Answer:
Therefore the annual rate of growth 9%.
Step-by-step explanation:
To find the annual rate, we use the following formula,
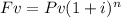
Fv= future value
Pv= present value.
i= rate of interest
n= time.
Here Pv=$250, Fv= $1,000, n= 16 years
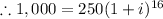
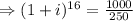
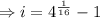
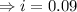 (approx)
(approx)
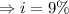
Therefore the annual rate of growth 9%.