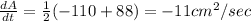Question

The base of a triangle is shrinking at a rate of 11 cm/s and the height of the triangle is increasing at a rate of 11 cm/s. Find the rate at which the area of the triangle changes when the height is 10cm and the base is 8cm.

Answer 1

The area of the triangle is decreasing at a rate 11 square centimeter per second

Explanation:`

We are given the following in the question:

`(db)/(dt) = -11\text{ cm per sec}\\\\(dh)/(dt) = 11\text{ cm per sec}`

Instant base = 8 cm

Instant height = 10 cm

Area of triangle =

`A = (1)/(2)* b * h`

where b is the base of the triangle and h is the height of the triangle.

Rate of change of area =

`(dA)/(at) = (1)/(2)(b(dh)/(dt) + h(db)/(dt))`

Putting values, we get,

`(dA)/(dt) = (1)/(2)(8(11) + (10)(-11))\\\\(dA)/(dt)=-11`

Thus, the area of the triangle is decreasing at a rate 11 square centimeter per second

Answer 2

the rate of changes of the area of the triangle

`(dA)/(dt) = -11 cm^2 /sec`

Explanation:

Explanation :-

The area of triangle( A) =
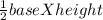`(1)/(2) base X height` ..........(1)

Let 'b' be the base and 'l' be the length of the triangle

The base of a triangle is shrinking( means decreasing) at a rate of 11 cm/s

that is
`(db)/(dt) = -11cm/sec`

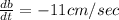
The height of a triangle is increasing at a rate of 11 cm/s

that is
`(dh)/(dt) = 11cm/sec`

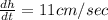
Given h= 10cm and b = 8cm

The rate of change of triangle

applying uv formula
`(d(uv))/(dx) = u( (dv)/(dx)) + v((du)/(dx) )`

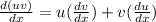
Differentiating equation (1) with respective to 't'

`(dA)/(dt) =(1)/(2) ( b((dh)/(dt) )+h ( (db)/(dt)))`

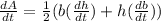
substitute all values in above equation, we get

h= 10cm , b = 8cm ,
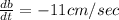`(db)/(dt) = -11cm/sec` and
`(dh)/(dt) = 11cm/sec`

`(dA)/(dt) = 10 (-11) + 8(11 )`

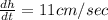
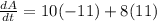
After simplification , we get

`(dA)/(dt) =(1)/(2) (-110 +88) = -11 cm^2 /sec`