Answer:
a)
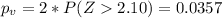
b)
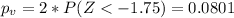
c)
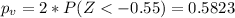
d)
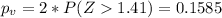
e)

Explanation:
Newly purchased tires of a particular type are supposed to be filled to a pressure of 30 psi. Let m denote the true average pressure. A test is to be carried out to decide whether m differs from the target value. Determine the P-value for each of the following z test statistic values.
System of hypothesis
We need to conduct a hypothesis in order to check if the true mean is different from m :
Null hypothesis:
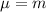
Alternative hypothesis:
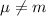
The statistic is given by
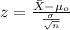 (1)
(1)
a. 2.10
Since is a bilateral test the p value is given by:
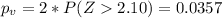
And we can use the following excel code:
"=2*(1-NORM.DIST(2.1,0,1,TRUE))"
b. -1.75
Since is a bilateral test the p value is given by:
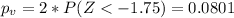
And we can use the following excel code:
"=2*(NORM.DIST(-1.75,0,1,TRUE))"
c. -.55
Since is a bilateral test the p value is given by:
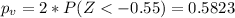
And we can use the following excel code:
"=2*(NORM.DIST(-0.55,0,1,TRUE))"
d. 1.41
Since is a bilateral test the p value is given by:
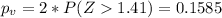
And we can use the following excel code:
"=2*(1-NORM.DIST(1.41,0,1,TRUE))"
e. -5.3
Since is a bilateral test the p value is given by:

And we can use the following excel code:
"=2*(NORM.DIST(-5.3,0,1,TRUE))"