Answer:
The standard error of the mean is 15
Explanation:
Given that a simple random sample of 64 observations was taken from a large population.
Hence it can be written as n=64
The population standard deviation is 120.
It can be written as

The sample mean was determined to be 320.
It can be written as
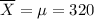
To find the standard error of the mean :
The formula for the standard error of the mean is given by
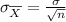
Now substitute the values in the formula we get
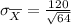


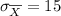
∴ The standard error of the mean is 15