Answer:
27.63 mph
Explanation:
First we find the distance, p between the Car and the house using Pythagoras theorem.

Taking derivatives of:
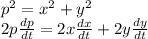
Since the farmhouse does not move, its speed
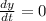
Therefore:
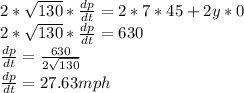
The distance between the automobile and the farmhouse is increasing at a rate of 27.63mph.