Answer:
Probability that a single student randomly chosen from all those taking the test scores 539 or higher is 0.5714.
Explanation:
We are given that the scores of students on the SAT college entrance examinations at a certain high school had a normal distribution with mean μ = 534 and standard deviation σ = 27.3.
Let X = scores of students on the SAT college entrance examinations
SO, X ~ N(
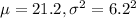 )
)
The z-score probability distribution is given by ;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean score = 534
= mean score = 534
 = standard deviation = 27.3
= standard deviation = 27.3
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
Now, the probability that a single student randomly chosen from all those taking the test scores 539 or higher is given by = P(X
 539)
539)
P(X
 539) = P(
539) = P(


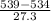 ) = P(Z
) = P(Z
 0.18)
0.18)
= 0.5714 {using z table}
Therefore, probability that a single student scores 539 or higher is 0.5714.