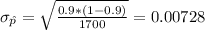Question

About 90% of young adult Internet users (ages 18 to 29) use social-networking sites. (a) Suppose a sample survey contacts an SRS of 1700 young adult Internet users and calculates the proportion pˆ in this sample who use social-networking sites. What is the approximate distribution of pˆ?

Answer 1

`\hat p \sim N(p ,\sqrt{(p(1-p))/(n)})`

With the following parameters

The mean is given by:

`\mu_(\hat p) = 0.9`

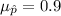
And the standard error is given by:

`\sigma_(\hat p)=\sqrt{(0.9*(1-0.9))/(1700)}= 0.00728`

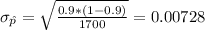
Explanation:

For this case we know that we have a sample size n = 1700

And the estimated proportion of young adult Internet users is 0.9

We can check the conditions in order to use the normal approximation:

1) np = 1700*0.9 = 1530>10

2) n(1-p) = 1700*(1-0.9)= 170>10

3) Randomization: The data comes from a random sample

For this case we assume that the three conditions are satisfied so then the normal approximation is useful and for this case is given by:

`\hat p \sim N(p ,\sqrt{(p(1-p))/(n)})`

With the following parameters

The mean is given by:

`\mu_(\hat p) = 0.9`

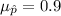
And the standard error is given by:

`\sigma_(\hat p)=\sqrt{(0.9*(1-0.9))/(1700)}= 0.00728`