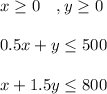Answer:
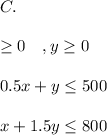
Explanation:
We first denote the inequalities of the number of shirts and skirts.
#Since you cannot make a negative number of shirts or skirts, the inequalities will be written as:
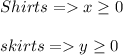
#We then represent the inequality of material.
-The material size is a production constraint as only 500 yards of material is available for use.
-The inequality is therefore written as:
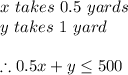
#We then represent the inequality of time.
-The material size is a production constraint as only 800 hours available for use.
-The inequality is therefore written as:
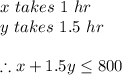
We combine the three inequalities to represent the constraints