Question

A 1000 Kg car approaches an intersection traveling north at 30 m/s . A 1250 Kg car approaches the same intersection traveling east at 39 m/s . The two cars collide at the intersection and lock together. Ignoring any external forces that act on the cars during the collision, what is the velocity of the cars immediately after the collision?

Answer 1

The final velocity has a magnitude of 25.44 m/s and is at 31.61° north of east.

Step-by-step explanation:

Taking north direction as positive y axis and east direction as positive x axis .

Given:

Mass of first car is,
`m_1=1000\ kg`

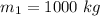
Initial velocity of first car is,
`u_1=30\vec{j}\ m/s`

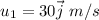
Mass of second car is,
`m_2=1250\ kg`

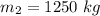
Initial velocity of second car is,

Let the combined final velocity after collision be 'v' m/s with as components of final velocity along east and north directions respectively.

Now, as the net external force is zero, momentum is conserved for the two car system along the east and north directions.

Conserving momentum along the east direction, we have:

Initial momentum = Final momentum

`m_1u_(1x)+m_2u_(2x)=(m_1+m_2)v_x\\\\0+1250* 39=(1000+1250)v_x\\\\v_x=(48750)/(2250)\\\\v_x=(65)/(3) m/s`

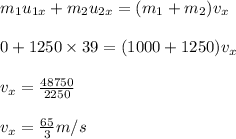
There is no component of initial velocity for first car in east direction, as it is moving in the north direction. So,

Now, conserving momentum along the north direction, we have:

Initial momentum = Final momentum

`m_1u_(1y)+m_2u_(2y)=(m_1+m_2)v_y\\\\1000* 30+0=(1000+1250)v_y\\\\v_y=(30000)/(2250)\\\\v_y=(40)/(3)\ m/s`

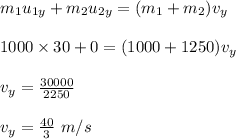
There is no component of initial velocity for second car in north direction, as it is moving in the east direction. So,
`u_(2y)=0`.

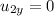The magnitude of final velocity is given as:

`|\vec{v}|=√((v_x)^2+(v_y)^2)\\\\|\vec{v}|=\sqrt{((65)/(3))^2+((40)/(3))^2}\\\\|\vec{v}|=\sqrt{(5825)/(9)}=25.44\ m/s`

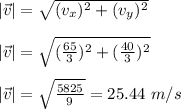
The direction is given as:

`\theta=\tan^(-1)((v_y)/(v_x))\\\\\theta=\tan^(-1)(((40)/(3))/((65)/(3)))=31.61^\circ`

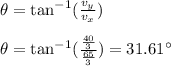
So, the final velocity has a magnitude of 25.44 m/s and is at 31.61° north of east.