Question

A writer makes on average one typographical error every page. The writer has landed a 3-page article in an important magazine. If the magazine editor finds any typographical errors, they probably will not ask the writer for any more material. What is the probability that the reporter made no typographical errors for the 3-page article?

Answer 1

That would be 5%

Explanation:

Answer 2

The probability that the reporter made no typographical errors for the 3-page article is 5%.

Explanation:

Let X = number of typographical errors made by the writer.

The average umber of mistakes mad by the writer every page is, E (X) = 1.

The random variable X is defined as finite number of occurrence of a certain activity in a fixed interval of time.

A Poisson distribution is used to describe the distribution of occurrences in a certain interval.

Thus, the random variable X follows a Poisson distribution.

It is provided that the writer has landed a 3-page article in an important magazine.

Then the average number of mistakes in the 3 pages is:

λ = 3 × E (X) = 3 × 1 = 3.

The probability mass function of the Poisson random variable X is:

`P(X=x)=(e^(-3)3^(x))/(x!);\ x=0,1,2,3...`

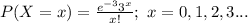
Compute the probability that the writer makes no mistake in a 3-page article as follows:

`P(X=0)=(e^(-3)3^(0))/(0!)=(0.0498* 1)/(1)=0.0498\approx 0.05`

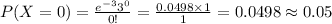
The probability that the writer makes no mistake in a 3-page article is 0.05.

Thus, the probability that the reporter made no typographical errors for the 3-page article is 5%.