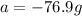Question

During her high bar routine from question 2, Gabby Douglas slipped and falls from the high bar, landing on a 10 cm thick gymnastics mat. She strikes the back of her head against the mat during her landing. Her head is moving at 7 m/s when it first strikes the mat. The mass of her head is 5 kg. The impact ends when her head comes to a stop after deflecting the mat 6.5 cm.

a. How much kinetic energy does her head have the instant just before it hits the mat?
b. How much work does the mat do to stop the motion of her head?
c. What average impact force exerted by the mat on her head during impact?
d. Estimate the peak impact force exerted by the moat on her head.
e. Eestimate the peak acceleration of her head.
f. Express the peak acceleration in g's.

Answer 1

a) 122.5 J

b) -122.5 J

c) -1884.6 N

d) -3769.2 N

e)
`-753.8 m/s^2`

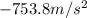
f)
`a=-76.9 g`

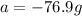
Step-by-step explanation:

a)

The kinetic energy of an object is the energy possessed by the object due to its motion.

Mathematically, it is given by:

`K=(1)/(2)mv^2`

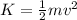
where

m is the mass of the object

v is the speed of the object

Here, we want to find the kinetic energy of the head just before hitting the mat.

At that instant, the speed is:

v = 7 m/s

The mass of the head is:

m = 5 kg

So, the kinetic energy is

`K=(1)/(2)(5)(7)^2=122.5 J`

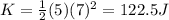
b)

According to the work-energy theorem, the work done by a force on an object is equal to the change in kinetic energy of the object:

`W=K_f - K_i`

where

W is the work done

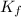`K_f` is the final kinetic energy

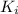`K_i` is the initial kinetic energy

In this problem:

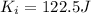`K_i=122.5 J` is the kinetic energy of the head just before hitting the mat

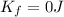`K_f=0 J` is the final kinetic energy (since the head comes to a stop)

So, the work done by the mat is:

`W=0-122.5 = -122.5 J`

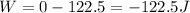
The work is negative because the force exerted by the mat is opposite to the direction of motion of the head.

c)

The work exerted by a force on an object is given by

`W=Fd`

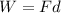
where

F is the force applied

d is the displacement of the object

W is the work done

In this problem:

W = -122.5 J is the work done by the mat on the head

d = 6.5 cm = 0.065 m is the displacement of the head (since it deflects the mat by this amount)

So, the average force exerted by the mat on the head is:

`F=(W)/(d)=(-122.5)/(0.065)=-1884.6 N`

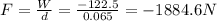
(the negative sign indicates that the force is in direction opposite to the motion of the head)

d)

The force calculated in part d) represents the average force exerted by the mat on the head:

`F_(avg)=-1884.6 N`

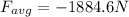
We can assume that as the head first hits the mat, the initial force is zero, then increases at a constant rate up to a peak value of
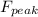`F_(peak)`, then it decreases again until the head stops.

In this case, the relationship between average force and peak force is:

`F_(avg)=(0+F_(peak))/(2)`

And therefore, the peak impact force exerted by the mat on the head is:

`F_(peak)=2F_(avg)=2(1884.6)=-3769.2 N`

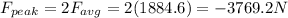
e)

The peak acceleration of the head can be found by using Newton's second law, which states that:

`F=ma`

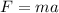
where

F is the force on the head

m is the mass of the head

a is the acceleration

Here we have:

F = -3769.2 N is the peak force

m = 5 kg is the mass of the head

So, solving for the acceleration, we find:

`a=(F)/(m)=(-3769.2)/(5)=-753.8 m/s^2`

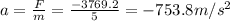
f)

The value of the acceleration due to gravity is

`g=9.8 m/s^2`

Here we want to express the peak acceleration of the head in terms of the acceleration due to gravity; so we can write:

`a=Ng`

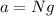
where

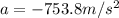`a=-753.8 m/s^2` is the peak acceleration

N is the ratio between the peak acceleration and the gravity acceleration

Solving for N,

`N=(a)/(g)=(-753.8)/(9.8)=-76.9`

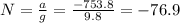
This means that the peak acceleration can be written as

`a=-76.9 g`