Question

ACCORDING TO THE FEBRUARY 2008 FEDERAL trade commission reports on consumer fraud and identity theft, Alaska had 321 complaints of identity theft out of 1,432 consumer complaints. Calculate 90% confidence interval

Answer 1

Answer: (0.205905, 0.242095)

Explanation:

We know that the confidence interval for population proportion is given by :-

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

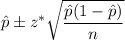
, where
`\hat{p}`= sample proportion

n= sample size

Let p be the proportion of complaints of identity theft .

As per given , we have

n= 1432

`\hat{p}=(321)/(1432)\approx0.224`

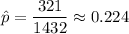
By standard normal table , z* = 1.645 for 90% confidence level.

Now , 90% confidence interval for p will be :

`0.224\pm (1.645)\sqrt{(0.224(1-0.224))/(1432)}\\\\=0.224\pm (1.645)(0.011)\\\\=0.224\pm 0.018095\\\\=(0.224-0.018095,\ 0.224+0.018095)\\\\=(0.205905,\ 0.242095)`

Hence, required confidence interval = (0.205905, 0.242095)