Answer: (0.205905, 0.242095)
Explanation:
We know that the confidence interval for population proportion is given by :-
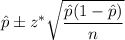
, where
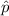 = sample proportion
= sample proportion
n= sample size
Let p be the proportion of complaints of identity theft .
As per given , we have
n= 1432
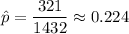
By standard normal table , z* = 1.645 for 90% confidence level.
Now , 90% confidence interval for p will be :

Hence, required confidence interval = (0.205905, 0.242095)