Question

The outer layer of cable on a cable reel is 16.2 cm from the center of the reel. The reel is initially stationary and can rotate about a fixed axis. It takes 3.6 seconds to pull off 3.7 meters of cable. Assume that the cable is pulled with a constant force (constant acceleration) and that the change in the effective radius is negligible.

How many revolutions did the reel make in 3.6 seconds? (no units)

Answer: 3.635

However, I am really having trouble figuring out parts B and C to this problem

B) What is the angular speed of the reel after 3.6 seconds?
(include units with answer)

C)What is the angular acceleration of the reel?
(include units with answer)

Answer 1

b)the angular speed after 3.6s is is 12.7rad/s

c) the angular acceleration of the reel is 3.52rad/s²

Step-by-step explanation:

b)

The angle in radian is represented as follows

`\theta = (L_t)/(r)`

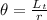
r = 16.2cm = 0.162m

`= (3.7)/(0.162) \\= 22.8radians`

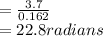
now,

`\theta=\omega_(0)t+(1)/(2)\alpha t^(2)`

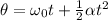
where

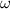`\omega` is the angular speed

`\alpha` is the angular acceleration

t is the time

`(22.8) = (0)(3.6)+(1)/(2) \alpha(3.6)^2\\\\\alpha = ((2)(22.8)/(3.6^2) \\\\= 3.52rad/s^2`

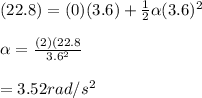
the first equation of motion is represeented by

`\omega=\omega _0+at`

`\omega= (0) + (3.52)(3.6)\\= 12.7rad/s`

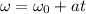
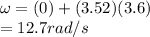
the angular speed after 3.6s is is 12.7rad/s

c)

from the above calculation , angular acceleration is calculated as

`\omega =3.52rad/s^2`

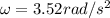
Therefore, the angular acceleration of the reel is 3.52rad/s²

Answer 2

B. w=12.68rad/s

C. α=3.52rad/s^2

Step-by-step explanation:

B)

We can solve this problem by taking into account that (as in the uniformly accelerated motion)

`\theta=\omega_(0)t+(1)/(2)\alpha t^(2)\\\theta = (s)/(r)` ( 1 )

where w0 is the initial angular speed, α is the angular acceleration, s is the arc length and r is the radius.

In this case s=3.7m, r=16.2cm=0.162m, t=3.6s and w0=0. Hence, by using the equations (1) we have

`\theta=(3.7m)/(0.162m)=22.83rad`

`22.83rad=(1)/(2)\alpha (3.6s)^2\\\\\alpha=2((22.83rad))/(3.6^2s)=3.52(rad)/(s^2)`

to calculate the angular speed w we can use
`\alpha=(\omega _(f)-\omega _(i))/(t _(f)-t _(i))\\\\\omega_(f)=\alpha t_(f)=(3.52(rad)/(s^2))(3.6)=12.68(rad)/(s)`

Thus, wf=12.68rad/s

C) We can use our result in B)

`\alpha=3.52(rad)/(s^2)`

I hope this is useful for you

regards