Answer:
We need at least 271 transactions
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
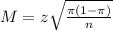
90% confidence level
So
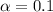 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
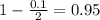 , so
, so
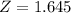 .
.
Minimum sample size within five percentage points.
n when M = 0.05.
We dont know the proportion, so we use
 , which would be the proportion requiring the largest sample size
, which would be the proportion requiring the largest sample size
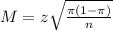
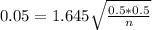
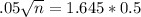
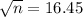

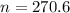
Rouding up
We need at least 271 transactions