Answer:
31.232 kJ
Step-by-step explanation:
Given,
mass of the particle, m = 4 Kg
Position of object as the function of time
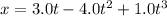
Work done by the object by the force from t = 0 to t = 8.0 s =?
we know,
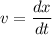

velocity at t = 0 s
u = 3 - 8 x 0 + 3 x 0 = 3 m/s
velocity at t= 8 s
v = 3 - 8 x 8 + 3 x 8 x 8
v = 125 m/s
Work done is equal to change in KE

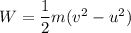
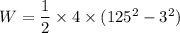
W = 31.232 k J
Hence, work done is equal to 31.232 kJ