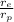Answer:
Answer:
a) ratio of radii for same momentum = 1
b) ratio of radii for same energy = 2.3 ×
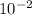
Step-by-step explanation:
using formula for radius
r =

where m is mass
v is velocity
q is charge
B is magnetic field
a) for same momentum radius will be inversely proportional to roduct of charge and magnetic and magnetic field
r ∝
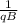
since for proton and electron s charge and magnetic field is same so
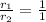
b) using relation b/w kinetic energy and momentum
p =
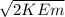 ............(1)
............(1)
where p is momentum and
K.E is kinetic energy
we know
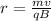
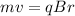
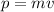 =
=
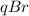
from first equation
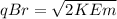
since qB is same for electron and proton and energy is also same(given)
so we get