Answer:
Option C) 16%
Explanation:
We are given the following information in the question:
Mean, μ = 100
Standard Deviation, σ = 18
We are given that the distribution of IQ score is a bell shaped distribution that is a normal distribution.
Empirical Formula:
- Almost all the data lies within three standard deviation from the mean for a normally distributed data.
- About 68% of data lies within one standard deviation from the mean.
- About 95% of data lies within two standard deviations of the mean.
- About 99.7% of data lies within three standard deviation of the mean.
We have to find the percentage of data above 118.
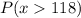

From empirical rule we can write:
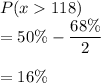
Thus, the correct answer is
Option C) 16%