Question

Of 560 samples of seafood purchased from various kinds of food stores in different regions of a country and genetically compared to standard gene fragments that can identify the​ species, 56​% were mislabeled. ​a) Construct a 90​% confidence interval for the proportion of all seafood sold in the country that is mislabeled or misidentified. ​b) Explain what your confidence interval says about seafood sold in the country. ​c) A government spokesperson claimed that the sample size was too​ small, relative to the billions of pieces of seafood sold each​ year, to generalize. Is this criticism​ valid?

Answer 1

a) (0.5256,0.5944)

c) Criticism is invalid

Explanation:

We are given the following in the question:

Sample size, n = 560

Proportion of mislabeled = 56%

`\hat{p} = 0.56`

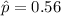
a) 90% Confidence interval:

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = \pm 1.64`

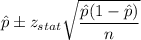
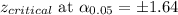
Putting the values, we get:

`0.56\pm 1.64(\sqrt{(0.56(1-0.56))/(560)}) = 0.56\pm 0.0344\\\\=(0.5256,0.5944)`

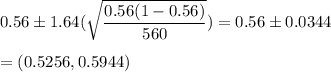
b) Interpretation of confidence interval:

We are 90% confident that the true proportion of all seafood in the country that is mislabeled or misidentified is between 0.5256 and 0.5944 that is 52.56% and 59.44%.

c) Validity of criticism

Conditions for validity:

`np > 10\\n(1-p)>10`

Verification:

`560* 0.56 = 313.6>10\\560(1-0.56) = 246.4>10`

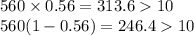
Both the conditions are satisfied. This, the criticism is invalid.