Answer:
When he weight of the car is 8.55 x
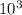 N then power = 314.012 KW
N then power = 314.012 KW
When he weight of the car is 1.10 x
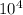 N then power = 43.76 KW
N then power = 43.76 KW
Step-by-step explanation:
Given that
Initial velocity
 = 0
= 0
Final velocity
 = 24.8
= 24.8

Time = 7.88 sec
We know that power required to accelerate the car is given by
P =
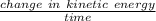
Change in kinetic energy Δ K.E =
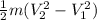
Since Initial velocity
 = 0
= 0
⇒ Δ K.E =

⇒ Power P =
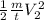
⇒ Power P =
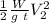 -------- (1)
-------- (1)
(a). The weight of the car is 8.55 x
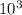 N = 8550 N
N = 8550 N
Put all the values in above formula
So power P =
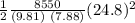
P = 314.012 KW
(b). The weight of the car is 1.10 x
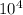 N = 11000 N
N = 11000 N
Put all the values in equation (1) we get
P =
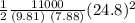
P = 43.76 KW