Question

In choice situations of this type, subjects often exhibit the "center stage effect," which is a tendency to choose the item in the center. In this experiment, 34 subjects chose the pair of socks in the center. What is the probability, P , that 34 or more subjects would choose the item in the center if each subject were selecting his or her preferred pair of socks at random? Use the Normal approximation first. If your software allows, find the exact binomial probability, Pe , and compare the two. (Enter your answers rounded to four decimal places.)

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

The probability that he or she would choose the pair of socks in the center position is
`p =(1)/(5)`

The correct answer choice is

X has a binomial distribution with parameters n=100 and p=1/5

b

The mean is
`\mu = 20`

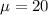
The standard deviation is
`\sigma=4`

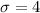
c

The probability,
`P =0.0002`

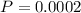
d

The correct answer is

The experiment supports the center stage effect. If participants were truly picking the socks at random, it would be highly unlikely for 34 or more to choose the center pair.

Using the R the probability
`Pe = 0.0003`

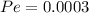
The probabilities
`P \approx Pe`

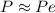
Explanation:

Since the person selects his or her desired pair of socks at random , then the probability that the person would choose the pair of socks in the center position from all the five identical pair is mathematically evaluated as

`p =(1)/(5)`

`=0.2`

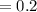
The mean of this distribution is mathematical represented as

`\mu = np`

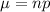
substituting the value

`\mu = 100 * 0.2`

`\mu = 20`

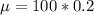
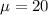
The standard deviation is mathematically represented as

`\sigma = √(np (1-p))`

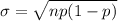
substituting the value

`= √(100 * 0,2 (1-0.2))`

`\sigma=4`

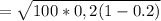
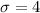
Applying normal approximation the probability that 34 or more subjects would choose the item in the center if each subject were selecting his or her preferred pair of socks at random would be mathematically represented as

`P=P(X \ge 34 )`

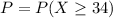
By standardizing the normal approximation we have that

`P(X \ge 34) \approx P(Z \ge z)`

Now z is mathematically evaluated as

`z = (x-\mu)/(\sigma )`

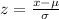
Substituting values

`z = (34-20)/(4)`

`=3.5`

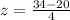
So using the z table the
`P(Z \ge 3.5)` is 0.0002

The probability P and Pe that 34 or more subject would choose the center pair is very small So

The correct answer is

The experiment supports the center stage effect. If participants were truly picking the socks at random, it would be highly unlikely for 34 or more to choose the center pair.