Answer:
Probability that the sample mean would be less than 23,013 dollars is 0.2358.
Explanation:
We are given that the mean per capita income is 23,037 dollars per annum with a variance of 149,769.
Also, a sample of 134 persons is randomly selected.
Firstly, Let
 = sample mean
= sample mean
The z-score probability distribution for sample mean is given by;
Z =
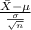 ~ N(0,1)
~ N(0,1)
where,
 = population mean per capita income = 23,037 dollars p.a.
= population mean per capita income = 23,037 dollars p.a.
 = standard deviation =
= standard deviation =
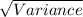 =
=
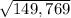 = 387 dollars p.a
= 387 dollars p.a
n = sample of persons = 134
So, probability that the sample mean would be less than 23,013 dollars is given by = P(
 < 23,013 dollars)
< 23,013 dollars)
P(
 < 23,013) = P(
< 23,013) = P(
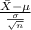 <
<
 ) = P(Z < -0.72) = 1 - P(Z
) = P(Z < -0.72) = 1 - P(Z
 0.72)
0.72)
= 1 - 0.7642 = 0.2358
The above probability is calculated using the z-score table.
Therefore, probability that the sample mean would be less than 23013 dollars if a sample of 134 persons is randomly selected is 0.2358.