Question

A solid sphere of radius R has a constant charge distribution, r, throughout its volume. Calculate the electric potential, V(r =0), at the center of the sphere assuming that infinitely far away V(r =[infinity]) = 0.

Answer 1

V(0)=3Q/(8*pi*ε0R)

Step-by-step explanation:

To find the values of the potential inside the solid sphere we have to use

`V(r)=-\int E \cdot dr`

`E=(Q)/(4\pi \epsilon_0 r^2)\hat{r}`

and we have also to take the charge density of the sphere as

`\rho=(Q)/(V)=(Q)/(4\pi R^3/3)=(3Q)/(4\pi R^3)`

we can integrate from r to R (the radius of the solid sphere)

`V=-\int (Q)/(4\pi \epsilon_0 r^2)dr=-\int_r^R (1)/(3\epsilon_0)\rho rdr\\\\V=-(\rho)/(3\epsilon_0)((R^2)/(2)-(r^2)/(2))=(Q(3R^2-r^2))/(8\pi \epsilon_0R^3)\\\\V(0)=(3QR^2)/(8\pi \epsilon_0 R^3)=(3Q)/(8\pi \epsilon_0 R)`

hope this helps!!

Answer 2

Vb = k Q / 2R

Step-by-step explanation:

To calculate the electric potential we use the relationship with the electric potential

dV = E. ds

Therefore we must find the electric potential for the interior of the sphere, for which we can use Gauss's law.

Ф = E .dA =
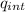`q_(int)` / ε₀

We define a Gaussian surface as a sphere of radius r, in this case the electric field lines and the radial lines of the sphere are parallel so the scalar product is reduced to the algebraic product

The area to a sphere is

A = 4π R²

E A = q_{int} /ε₀

Let's use constant charge density

ρ = q_{int} / V

V = 4/3 π r³

q_{int} = ρ 4/3 π r³

We substitute

E = (ρ 4/3 π r³) / 4π r² ε₀

E = ρ / 3ε₀ r

Now we can find electrical potential

.dV = - ρ / 3ε₀ ∫ r dr

Vb –Va = - ρ / 3ε₀ r² / 2

We evaluate between the lower limits r = R and the upper limit r = r

Vb –Va = ρ / 3ε₀ (R² - r²) / 2

We substitute the density value

ρ = Q / (4/3 π R³)

Vb- Va = Q (1 / 4πε₀) (R²-r²) / 2R³

Where

k = 1 / 4π ε₀

Vb-Va = k Q / 2R³ (R² - r²)

In the center of the sphere r = 0

Vb = k Q / 2R