Question

An element with a mass of 980 grams decays by 10.5% per minute. To the nearest tenth of a minute, how long will it be until there are 380 grams of the element remaining?

Answer 1

About 8.5 mins

Explanation:

This is a compound decay problem, which goes by the formula:

`F=P(1-r)^t`

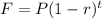
Where

F is the future amount (we want it to be 380)

P is the present amount (980 now)

r is the rate of decay per minute (10.5% = 10.5/100 = 0.105)

t is the time it takes (what we want to find)

Substituting, we get our answer to be:

`F=P(1-r)^t\\380=980(1-0.105)^t\\380=980(0.895)^t\\0.3878=0.895^t\\Ln(0.3878)=Ln(0.895^t)\\Ln(0.3878)=t*Ln(0.895)\\t=(Ln(0.3878))/(Ln(0.895))\\t=8.54`

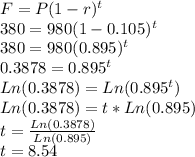
SO, it is going to take about 8.54 mins, rounded to nearest tenth (1 decimal), we have:

About 8.5 mins