Question

An alpha particle (the nucleus of a helium atom) consists of two protons and two neutrons, and has a mass of 6.64 * 10-27 kg. A horizontal beam of alpha particles is injected with a speed of 1.3 * 105 m>s into a region with a vertical magnetic field of magnitude 0.155 T. (a) How much time does it take for an alpha particle to move halfway through a complete circle

Answer 1

t = 4.21x10⁻⁷ s

Step-by-step explanation:

The time (t) can be found using the angular velocity (ω):

`\omega = (\theta)/(t)`

Where θ: is the angular displacement = π (since it moves halfway through a complete circle)

We have:

`t = (\theta)/(\omega) = (\theta)/(v/r)`

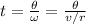
Where:

v: is the tangential speed

r: is the radius

The radius can be found equaling the magnetic force with the centripetal force:

`qvB = (mv^(2))/(r) \rightarrow r = (mv)/(qB)`

Where:

m: is the mass of the alpha particle = 6.64x10⁻²⁷ kg

q: is the charge of the alpha particle = 2*p (proton) = 2*1.6x10⁻¹⁹C

B: is the magnetic field = 0.155 T

Hence, the time is:

`t = (\theta*r)/(v) = (\theta)/(v)*(mv)/(qB) = (\theta m)/(qB) = (\pi * 6.64 \cdot 10^(-27) kg)/(2*1.6 \cdot 10^(-19) C*0.155 T) = 4.21 \cdot 10^(-7) s`

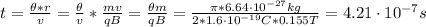
Therefore, the time that takes for an alpha particle to move halfway through a complete circle is 4.21x10⁻⁷ s.

I hope it helps you!