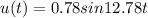Question

A mass of 148g stretches a spring 6cm. The mass is set in motion from its equlibrium position with a downward velocity of 10cm/s and no damping is applied. Determine the position u of the mass at any time t. Use 9.8m/s2 as the acceleration due to gravity. Pay close attention to the units.

Answer 1

`u(t)=0.78sin12.78t`

Step-by-step explanation:

We are given that

Mass,m=148 g

Length,L=6 cm

Velocity,u'(0)=10 cm/s

We have to find the position u of the mass at any time t

We know that

`\omega_0=\sqrt{(g)/(L)}=\sqrt{(980)/(6)}=12.78 rad/s`

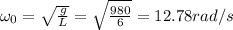
Where g=
`980 cm/s^2`

`u(t)=Acos12.78 t+Bsin 12.78t`

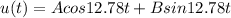
u(0)=0

Substitute the value

`A=0`

`u'(t)=-12.78Asin12.78t+12.78 Bcos12.78 t`

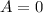
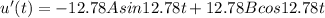
Substitute u'(0)=10

`12.78B=10`

`B=(10)/(12.78)=0.78`

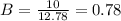
Substitute the values

`u(t)=0.78sin12.78t`