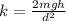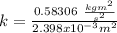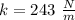Question

A(n) 55.5 g ball is dropped from a height of 53.6 cm above a spring of negligible mass. The ball compresses the spring to a maximum displacement of 4.89697 cm. The acceleration of gravity is 9.8 m/s 2 . x h Calculate the spring force constant k.

Answer 1

The spring force constant is
`k=243\ (N)/(m)` .

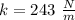Step-by-step explanation:

We are told the mass of the ball is
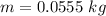`m=0.0555\ kg`, the height above the spring where the ball is dropped is
`h=0.536\ m`, the length the ball compresses the spring is
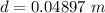`d=0.04897\ m` and the acceleration of gravity is
`9.8\ (m)/(s^(2))` .

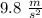We will consider the initial moment to be when the ball is dropped and the final moment to be when the ball stops, compressing the spring. We supose that there is no friction so the initial mechanical energy
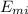`E_(mi)` is equal to the final mechanical energy
`E_(mf)` :

`E_(mf)=E_(mi)`

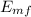Initially there is only gravitational potential energy because the force of the spring isn't present and the speed is zero. In the final moment there is only elastic potential energy because the height is zero and the ball has stopped. So we have that:

`(1)/(2)kd^(2)=mgh`

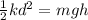
If we manipulate the equation we have that:

`k=(2mgh)/(d^(2) )`

`k=(2\ 0.0555\ kg\ 9.8(m)/(s^(2))\ 0.536\ m)/((0.04897)^(2)m^(2))`

`k=(0.58306\ (kgm^(2))/(s^(2)))/(2.398x10^(-3)m^(2))`

`k=243\ (N)/(m)`