Answer:
The value of final velocity of the first hockey puck
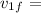 2.3
2.3

Step-by-step explanation:
Mass of hockey puck = m
Initial velocity
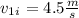
From conservation of momentum principal
4.5 m = m
 + m ×
+ m ×
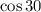 × 3.5
× 3.5
 = 1.5
= 1.5

0 = m
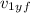 + m ×
+ m ×
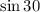 × 3.5
× 3.5
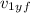 = - 1.75
= - 1.75

Now final velocity of first puck
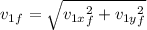
Put the values in above formula we get
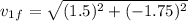
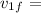 2.3
2.3

This is the value of final velocity of the first hockey puck.