Question

A 12.0-g bullet is fired horizontally into a 114-g wooden block that is initially at rest on a frictionless horizontal surface and connected to a spring having spring constant 146 N/m. The bullet becomes embedded in the block. If the bullet-block system compresses the spring by a maximum of 75.5 cm, what was the speed of the bullet at impact with the block

Answer 1

The speed of the bullet-block is
`V=0.81 ms^(-1)`.

Step-by-step explanation:

The expression of the conservation of energy to the given system is as follows;

`KE_i+PE_i=KE_f+PE_f`

Here,
`KE_i,KE_f` are the initial kinetic energy and final kinetic energy and
`PE_i,PE_f`.

`(1)/(2)mv^(2)+(1)/(2)kx^(2)=(1)/(2)(m+M)V^2+0`

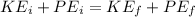
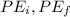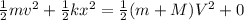
Here, m is the mass of the bullet, M is the mass of the wooden block, k is the spring constant, x is the distance, v is the speed of the bullet and V is the speed of the bullet with the block.

Calculate the speed of the bullet-block.

Convert the distance from cm to m.

x=75.5 cm

x=0.755 m

Put m= 12 g, M=114 g, v=0, x= 0.755 m and
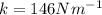`k=146 Nm^(-1)` in the above expression according to the given values in the problem.

`(1)/(2)(12)(0)^(2)+(1)/(2)(146)(0.755)^(2)=(1)/(2)(12+114)V^2+0`

`(1)/(2)(146)(0.755)^(2)=(1)/(2)(12+114)V^2`

`V=0.81 ms^(-1)`

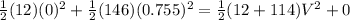
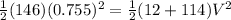
Therefore, the speed of the bullet-block is
`V=0.81 ms^(-1)`.