Answer:
Therefore the asteroids's orbital period is 7.45 years.
Step-by-step explanation:
Kapler's third law:
The orbital period of a planet squared is directly proportional to the average distance of the planet from the sun cubed.
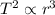
T = orbital period of the planet
r = orbital radius of the planet
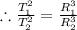
Here
 = Orbital period of the asteroid
= Orbital period of the asteroid
 = Orbital radius of the asteroid
= Orbital radius of the asteroid
 Orbital period of Earth = 1 year
Orbital period of Earth = 1 year
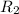 =Orbital radius of Earth
=Orbital radius of Earth
Given that the orbital radius of asteroid is 3.83 times of orbital radius of Earth.


Therefore
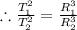
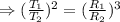
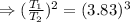
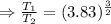
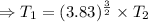
 [
[
 1 year]
1 year]

Therefore the asteroids's orbital period is 7.45 years.