Question

Washers The life span of a type of automatic washer is approximately normally distributed with mean and standard deviation equal to and years, respectively. If this type of washer is guaranteed for a period of years, what fraction will need to be repaired and/or replaced?

Answer 1

The fraction of washer that will need repair or replacement within the guarantee period is 3.4%.

Explanation:

Let X = lifespan of automatic washer (in years).

The lifespan of automatic washer is normally distributed with mean lifespan, μ = 10.5 years and standard deviation σ = 3 years.

To compute the probability of a normal distribution it is better to standardize the raw scores (X).

The raw score can be standardized using the formula:

`z=(X-\mu)/(\sigma)`

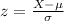
These standardized scores are known as z-scores.

The distribution of z-scores follows a normal distribution with mean 0 and variance 1. The distribution is also known as Standard Normal distribution.

Now, it is provided that this type of washer has a guarantee period of 5 years, i.e. within 5 years it would either need repair or replacement.

Compute the probability that the washer will need repair or replacement within 5 years as follows:

`P(X<5)=P((X-\mu)/(\sigma)<(5-10.5)/(3))\\`

`=P(Z<-1.83)\\=1-P(Z<1.83)\\=1-0.9664\\=0.0336\\\approx 3.4\%`

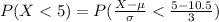
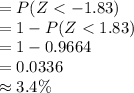
Thus, the fraction of washer that will need repair or replacement within the guarantee period is 3.4%.