Answer:
The value of poisson's ratio of the material = 0.28
Step-by-step explanation:
Given data
Force F = 15700 N
Diameter D = 8 mm
Change in diameter ΔD = 0.005 mm
Modulus of elasticity E = 140 ×
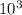 M Pa.
M Pa.
Stress induced in the shaft due to applied force
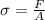
Area A =
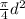
⇒ A =
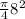 = 50.24
= 50.24
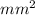
Now stress
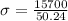
⇒ Stress
 = 312.5 M pa ------ (1)
= 312.5 M pa ------ (1)
Now strain in the element is given by
∈
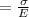
⇒ ∈ =
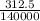
⇒ Strain ∈ = 2.232 ×

We know that poisson's ratio is given by
⇒
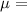
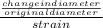
Change in diameter ΔD = 0.005 mm
Diameter D = 8 mm
Strain ∈ = 2.232 ×

⇒
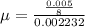
⇒
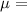 0.28
0.28
This is the value of poisson's ratio of the material.