Question

a genetic experiment with peas resulted in one sample of offspring that consisted of 418 green peas and 151 yellow peas. a.) construct a 95% confidence interval to estimate the percentage of yellow peas. b.) interpret this interval

Answer 1

95% Confidence interval: (0.2291,0.3015)

Explanation:

We are given the following in the question:

Sample size, n = 418+151 = 569

Number of yellow peas, x = 151

`\hat{p} = (x)/(n) = (151)/(569) = 0.2653`

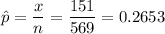
a) 95% Confidence interval:

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

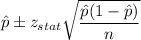
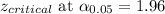
Putting the values, we get:

`0.2653\pm 1.96(\sqrt{(0.2653(1-0.2653))/(569)}) = 0.2653\pm 0.0362\\\\=(0.2291,0.3015)`

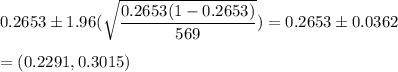
b) Interpretation of confidence interval

We are 95% confident that the proportion of yellow peas in the sample lies within the range (0.2291,0.3015)