Answer:
1.57 kg
Step-by-step explanation:
Let the mass of block is m.
Spring constant, K = 9.4 N/m
Amplitude, A = 15.5 cm
y = A/2
v = 32.8 cm/s = 0.328 m/s
The velocity of the particle executing SHM is given by

where, ω is the angular frequency of SHM.

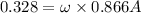
0.328 = ω x 0.866 x 0.155
ω = 2.45 rad/s
Now the angular frequency is given by

K = mω²
9.4 = m x 2.45 x 2.45
m = 1.57 kg