Question

Assume the number of typo errors on a single page of a book follows Poisson distribution with parameter 1=3. Calculate the probability that on one page there are (i) exactly 2 typos (ii) two or more typo?

Answer 1

(i). 0.03981

(ii).0.0048

Explanation:

The probability density function of Poisson distribution is:

`P(X=x,\lambda)=(e^(-\lambda)\lambda^x)/(x!) \; \;\;\,\; x=0,1,2,...`

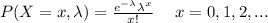
Consider X is a number of typos error on a single page of a book and X follows the Poisson distribution with
`\lambda = (1)/(3)`

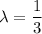
(i) Exactly two typos:

`\begin{aligned}P(X = 2,(1)/(3))&=\frac{e^{-(1)/(3)}(1)/(3)^(2)}{2!}\\&=\frac{e^{-(1)/(3)}}{18}\\&=0.03981\end{aligned}`

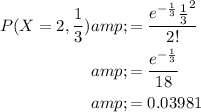
(ii) Two or more typos:

`\begin{aligned}P(X\geq2,(1)/(3))&=1-[P(X=0)+P(X=1)+P(X+2)]\\&=1-[0.7165+0.2388+0.03981]\\&=1-0.9952\\&=0.0048\end{aligned}`