Question

Light with a wavelength of (465 A) nm is incident on a metal surface with a work function of (1.25 (0.1)(B)) eV. Find the maximum kinetic energy of the emitted photoelectrons. Give your answer in eV and with 3 significant figures.

Answer 1

The maximum kinetic energy of photoelectrons is 3.02 eV

Step-by-step explanation:

Given:

Wavelength of light
`\lambda = 465 * 10^(-9)` m

Work function
`\phi = 1.25` eV

From the theory of photoelectric effect,

`KE_(max) = hf - \phi`

Where
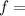`f =` frequency of light,
`\phi` = work function its depends on nature of metal.

`hf = (hc)/(\lambda) = (6.626 * 10^(-34) * 3 * 10^(8) )/(465 * 10^(-9) )`

`= 0.0427 * 10^(-17)`

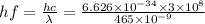
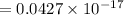
Now we convert energy in terms of electrovolt,

`hf = (0.0427 * 10^(-17) )/(1.6 * 10^(-19) )`

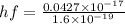
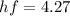`hf = 4.27` eV

Put above value,

`KE_(max) = 4.27 -1.25`

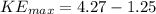
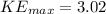`KE_(max) = 3.02` eV

Therefore, the maximum kinetic energy of photoelectrons is 3.02 eV