Question

Determine the rate at which the electric field changes between the round plates of a capacitor, 5.8 cm in diameter, if the plates are spaced 1.2 mm apart and the voltage across them is changing at a rate of 150 V/s.

Answer 1

The rate at which the electric field changes between the round plates of a capacitor is
`125* 10^(3)Vs^(-1)`.

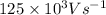Step-by-step explanation:

It is given in the problem that the round plates of a capacitor are spaced some distance apart and the voltage across them is changing.

The expression for the electric field in terms of voltage is as follows;

`E=(V)/(d)`

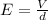
Here, E is the electric field, V is the voltage and d is the distance of separation.

Differentiate expression of the electric field with respect to time, t.

`(dE)/(dt)=(1)/(d)(dV)/(dt)`

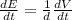
Convert the distance of separation from mm to m.

d= 1.2 mm

`d=1.2* 10^(-3)m`

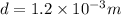
Calculate the rate at which the electric field changes.

`(dE)/(dt)=(1)/(d)(dV)/(dt)`

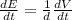
Put
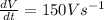`(dV)/(dt)=150 Vs^(-1)` and
`d=1.2* 10^(-3)m`

`(dE)/(dt)=(1)/(1.2* 10^(-3))(150)`

`(dE)/(dt)=125* 10^(3)Vs^(-1)`

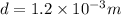
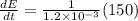
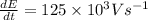
Therefore, the rate at which the electric field changes is
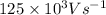`125* 10^(3)Vs^(-1)`.