Question

A wheel of radius 0.5 m rotates with a constant angular speed about an axis perpendicular to its center. A point on the wheel that is 0.2 m from the center has a tangential speed of 2 m/s. Determine the tangential acceleration of the point that is 0.2 m from the center.

Answer 1

The tangential acceleration is 0 m/s².

Step-by-step explanation:

Given:

Radius of the wheel = 0.5 m

The point of observation for calculating tangential acceleration = 0.2 m from center.

Tangential speed at the point of observation = 2 m/s

The angular speed of the wheel is a constant.

In order to determine the tangential acceleration, we make use of the following formula:

Tangential acceleration at a point = Angular acceleration × Distance of the point from center

Or,
`a_t=\alpha * r`

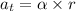
Now, angular acceleration is defined as the rate of change of angular speed.

Here, the angular speed of the wheel is a constant. So, the change of angular speed is 0. Therefore, the angular acceleration is also 0 rad/s².

Now, from the above formula, as angular acceleration is 0, the magnitude of tangential acceleration at a point that is 0.2 m from the center of the wheel is also 0 m/s².