Question

Two parallel plates have equal and opposite charges. When the space between the plates is evacuated, the electric field between the plates is E~ = 3.20 × 105 N/C. When the space is filled with a dielectric, the electric field is E~ = 2.50 × 105 N/C. What is the dielectric constant of this dielectric?

Answer 1

1.28

Step-by-step explanation:

Electric field between the plates when the separation between the plates is air, Eo = 3.20 x 10^5 N/C

Electric field between the plates when the separation between the plates is dielectric, E = 2.5 x 10^5 N/C

Let K is the dielectric constant

By the definition of dielectric constant, it is the ratio of electric field in the vacuum to the electric field when the dielectric is placed.

`K =(E_(0))/(E)`

`K = (3.20* 10^(5))/(2.5* 10^(5))`

K = 1.28

Thus, the dielectric constant of the material between the plates is 1.28.

Answer 2

The dielectric constant of this dielectric is 1.28.

Step-by-step explanation:

Given that,

When the space between the plates is evacuated, the electric field between the plates,
`E_o=3.2* 10^5\ N/C`

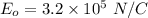
When the space is filled with a dielectric, the electric field is,
`E=2.5* 10^5\ N/C`

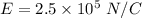
Let k is the dielectric constant of this dielectric. The electric field gets decreased by a factor of k if a dielectric is inserted between plates. So,

`k=(E_o)/(E)\\\\k=(3.2* 10^5)/(2.5* 10^5)\\\\k=1.28`

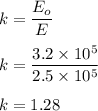
So, the dielectric constant of this dielectric is 1.28. Hence, this is the required solution.