Question

A 90 kg ice skater moving at 12.0 m/s on the ice encounters a region of roughed up ice with a coefficient of kinetic friction of 0.490. How far along the rough ice does she go before stopping?

Answer 1

The skater covers a distance of 15 m before stopping.

Step-by-step explanation:

Let the distance traveled before stopping be 'd' m.

Given:

Mass of the skater (m) = 90 kg

Initial velocity of the skater (u) = 12.0 m/s

Final velocity of the skater (v) = 0 m/s (Stops finally)

Coefficient of kinetic friction (μ) = 0.490

Acceleration due to gravity (g) = 9.8 m/s²

Now, we know that, from work-energy theorem, the work done by the net force on a body is equal to the change in its kinetic energy.

Here, the net force acting on the skater is only frictional force which acts in the direction opposite to motion.

Frictional force is given as:

`f=\mu N`

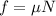
Where, 'N' is the normal force acting on the skater. As there is no vertical motion,
`N=mg`

∴
`f=\mu mg=0.490* 90* 9.8=432.18\ N`

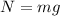
Now, work done by friction is a negative work as friction and displacement are in opposite direction and is given as:

`W=-fd=-432.18d`

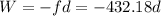
Now, change in kinetic energy is given as:

`\Delta K=(1)/(2)m(v^2-u^2)\\\\\Delta K=(1)/(2)* 90(0-12^2)\\\\\Delta K=45* (-144)=-6480\ J`

Therefore, from work-energy theorem,

`W=\Delta K\\\\-432.18d=6480\\\\d=(6480)/(432.18)\\\\d=14.99\approx 15\ m`

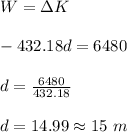
Hence, the skater covers a distance of 15 m before stopping.