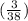Question

Choose the one alternative that best completes the statement or answers the question. A shipment of twenty radios contains six defective radios. Two radios are randomly selected from the shipment. 14) Find the probability that both radios selected are defective

Answer 1

The probability that both radios are defective =
`((3)/(38) )`

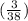
Explanation:

Here, the total number of radios = 20

The number of defective radios = 6

The number of radios selected at random = 2

P(Selecting first defective radio) =
`\frac{\textrm{Total favorable outcomes}}{\textrm{Total outcomes}} = (6)/(20) = ((3)/(10) )`

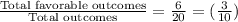
Now, after selecting first defective radio, total radios left = 20 - 1 = 19

Also, total defective radios = 6 - 1 = 5

P(Selecting second defective radio) =
`\frac{\textrm{Total favorable outcomes}}{\textrm{Total outcomes}} = ((5)/(19) )`

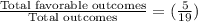
So, the combined probability of selecting 2 defective radios

`= ((3)/(10) ) * ((5)/(19) ) = ((3)/(38))`

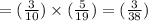
Hence, the probability that both radios are defective =
`((3)/(38) )`