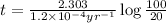Question

The decay constant for 14C is .00012 In 1947, the famous cave paintings in Lascaux, France were discovered and testing revealed that charcoal in the cave contained 20% of the 14C found in living trees. Write a formula for the age of the charcoal (hence of the associated paintings). Show your work to find this formula.

Answer 1

The question is incomplete, here is the complete question:

The decay constant for 14-C is
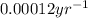`0.00012yr^(-1)` In 1947, the famous cave paintings in Lascaux, France were discovered and testing revealed that charcoal in the cave contained 20% of the 14-C found in living trees. Write a formula for the age of the charcoal (hence of the associated paintings). Show your work to find this formula.

Answer: The formula for the age of the charcoal is
`t=(2.303)/(1.2* 10^(-4)yr^(-1))\log (100)/(20)`

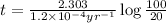
Step-by-step explanation:

Carbon-14 isotope is a radioisotope and its decay process follows first order kinetics.

Rate law expression for first order kinetics is given by the equation:

`k=(2.303)/(t)\log([A_o])/([A])`

where,

k = rate constant =
`0.00012yr^(-1)=1.2* 10^(-4)yr^(-1)`

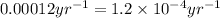
t = time taken for decay process = ? yr

`[A_o]` = initial amount of the sample = 100 grams

[A] = amount left after decay process = (100 - 20) = 80 grams

Putting values in above equation, we get:

`1.2* 10^(-4)=(2.303)/(t)\log(100)/(20)\\\\t=(2.303)/(1.2* 10^(-4)yr^(-1))\log (100)/(20)`

Hence, the formula for the age of the charcoal is
`t=(2.303)/(1.2* 10^(-4)yr^(-1))\log (100)/(20)`