Question

The arrival rate at a parking lot is 6 veh/ min. Vehicles start arriving at 6: 00 P. M., and when the queue reaches 36 vehicles, service begins. If company policy is that total vehicle delay should be equal to 500 veh-min, what is the departure rate? (Assume D/ D/ 1 queuing and a constant service rate.)

Answer 1

departure rate k = 7.653 vehicle per minute

Step-by-step explanation:

given data

parking = 6 veh/ min

arriving = 6: 00 P. M

queue reaches = 36 vehicles

total vehicle delay = 500 veh-min

solution

we know here that total vehicle in t min will be

total vehicle in t min = 6t vehicle

and

we consider here service rate is equal to departure rate

so service rate = k vehicle per min

and service is starting when reach vehicle 36

so that no of vehicle is

no of vehicle = 6t , ( 0 ≤ t ≤ 6 )

no of vehicle = 6t - k (t -6 ) for t ≥ 6

and

Queue dissipate when here 6t - k( t-6) will be zero

so

k =
`(6t)/(t-6)` ........................a

we know here

total delay is equal to 500 veh min

0.5 t × 6t - 0.5 (t-6) × k × (t-6) = 500

so solve it we get

t = 27.78 min

so k will be from equation a

k =
`(6* 27.78)/(27.78-6)`

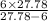
k = 7.653

so departure rate is 7.653 veh/min