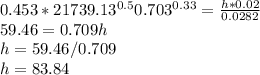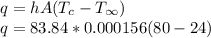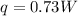Question

A square (12.5 mm × 12.5 mm) silicon chip is insulated on one side and cooled on the opposite side by atmospheric air in parallel flow at [infinity] 20 m/s and [infinity] 24°C. When in use, electrical power dissipation within the chip maintains a uniform heat flux at the cooled surface. Assume the critical Reynolds number is 5x105.

(a) If the chip temperature may not exceed 80°C at any point on its surface, what is the maximum allowable power?
(b) What is the maximum allowable power if the chip is flush mounted in a substrate that provides for an unheated starting length of 20 mm?

Answer 1

a) q = 0.927 W

b) q = 0.73 W

Step-by-step explanation:

Our assumptions are that:

• there is a steady state condition
• No heat loss during insulation
• No radiation
• Heat flux is uniform

`u_(\infty) = 20 m/s\\`

`T_(\infty) = 24^(0) C`

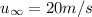
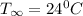
Chip temperature,
`T_(c) = 80^(0) C`

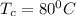
Temperature of the film,
`T_(f) = (T_(\infty)+ T_(c) )/(2) \\`

`T_(f) = (24 + 80)/(2) \\T_(f) = 52^(0) C`

`T_(f) = 52 + 273 K \\T_(f) = 325 K`

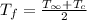
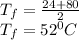
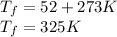
Atmospheric air is used to insulate the chip. i.e the film is an atmospheric air

1 atm of 325 K of air has the following properties:

viscosity, v = 18.4 × 10⁻⁶ m²/s

k = 0.0282 w/mk

Pr = 0.703

Nuselt number, Nu =
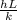`(hL )/(k)`..............(i)

Nu =
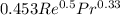`0.453Re^(0.5) Pr^(0.33)`................(2)

The Reynold number, Re, is calculated by the equation

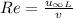`Re = (u_(\infty L) )/(v)`, L = 12.5 mm = 12.5 * 10⁻³ m

Re =
`(20 * 12.5 * 10^(-3) )/(18.4 * 10^(-6) )`

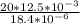
Re = 13586.96

Equating (1) and (2) and substituting necessary values

`0.453* 13586.96^(0.5) 0.703^(0.33) = (h * 12.5 * 10^(-3) )/(0.0282)` ..........(3)

47.006 = h * 0.4433

h = 47.006/0.4433

h = 106.05

The maximum allowable power is given by the equation,
`q = hA(T_(c)-T_(\infty) )`

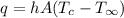
Area, A = length * Breadth = 0.0125*0.0125

A = 0.000156 m²

`q = 106.05*0.000156(80-24)\\q = 0.927 W`

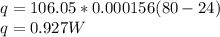
b) When the lenght, L = 20 mm = 0.02 m

Reynold number, Re =
`(20 * 0.02 )/(18.4 * 10^(-6) )`

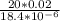
Re = 21739.13

By replacing Re and L, Equation (3) becomes:

`0.453* 21739.13^(0.5) 0.703^(0.33) = (h * 0.02 )/(0.0282)\\59.46 = 0.709h\\h = 59.46/0.709\\h = 83.84`

`q = hA(T_(c)-T_(\infty) )\\q = 83.84*0.000156(80-24 )`

`q = 0.73 W`