Question

ou place the spring vertically with one end on the floor. You then drop a book of mass 1.40 kgkg onto it from a height of 0.800 mm above the top of the spring. Find the maximum distance the spring will be compressed.

Answer 1

Complete question:

A spring of negligible mass has force constant k = 1600 N/m. (a) How far must the spring be compressed for 3.20 J of potential energy to be stored in it? (b) You place the spring vertically with one end on the floor. You then drop a 1.40-kg book onto it from a height of 0.800 m above the top of the spring. Find the maximum distance the spring will be compressed.

Answer:

(a) 0.063 m

(b) 0.126 m

Step-by-step explanation:

Given;

force constant, K = 1600 N/m

Part (a)

Elastic potential energy is given as;

U = ¹/₂Kx²

where;

x is the extension in the spring

`x = \sqrt{(2U)/(K) } = \sqrt{(2*3.2)/(1600) } = 0.063 \ m`

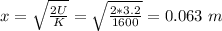
Part (b)

given;

mass of the book, m = 1.4 kg

height above the spring from which the book was dropped, h = 0.8 m

From the principle of conservation of energy;

Gravitational potential energy = Elastic potential energy

mgH = ¹/₂Kx²

H is the total vertical distance from floor to 0.8 m = maximum distance the spring will be compressed + h

let the maximum distance = A

mg(A+h) = ¹/₂KA²

1.4 x 9.8(A + 0.8) = ¹/₂ x 1600A²

13.72 (A + 0.8) = 800A²

13.72A + 10.976 = 800A²

800A² - 13.72A - 10.976 = 0

This is a quadratic equation, and we solve using formula method, where a = 800, b = - 13.72 and c = - 10.976

A = 0.126 m