Question

True or False: limx➡️0^+ e^-5/x =0

Answer 1

well, we can take a peek at this from the standpoint of moving from the right towards 0, but never getting there.

`e^{-(5)/(x)}\implies \cfrac{1}{e^{(5)/(x)}}\qquad \qquad \stackrel{x = 1}{\cfrac{1}{e^{(5)/(1)}}}\implies \cfrac{1}{e^5}\qquad \qquad \stackrel{x=0.000001}{\cfrac{1}{e^{(5)/(0.000001)}}}\implies \cfrac{1}{e^(500000)}`

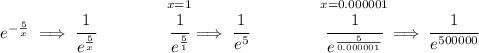
as "x" is moving towards 0, the denominator is becoming larger and ever larger, whilst the numerator is remaining the same, thus the fraction is become ever smaller, going towards = 0.