Answer:
63.750KeV
Step-by-step explanation:
We are given that
Initial velocity of second electron,
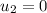
Radius,
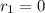
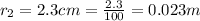
1 m=100 cm
Magnetic field,B=0.0370 T
We have to determine the energy of the incident electron.
Mass of electron,

Charge on an electron,
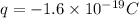
Velocity,
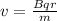
Using the formula
Speed of electron,
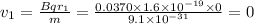
Speed of second electron,
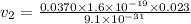
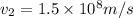
Kinetic energy of incident electron=
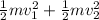
Kinetic energy of incident electron=

Kinetic energy of incident electron=
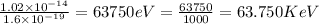
1KeV=1000eV