Answer:
$1100 per apartment
Step-by-step explanation:
For each x times increase by $20, x units goes vacant.
Thus,
We can say:
Rent is 400 + 20x
The number of apartments rented then is 90 - x
The revenue would be the rent multiplied by the number of apartments rented. So revenue would be:

This is a parabola with a = 1 , b = -70, and c = -1800
THe max value occurs at
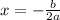
SO, that would be at:
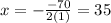
Hence, if there is "35" increases of $20, that would give us the max revenue.
35 number of increases of $20 means:
20*35 = 700 increase
So, rent should be set at 400 + 700 = $1100 per apartment