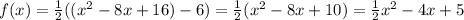Question

Find the equation, (f(x) = a(x - h)2 + k), for a parabola containing point (2, -1) and having (4, -3) as a vertex. What is the standard form of the equation?

Answer 1

`f(x)=(1)/(2)x^2-4x+5`

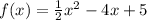
Explanation:

A parabola is written in the form

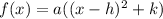`f(x)=a((x-h)^2+k)` (1)

where:

`h` is the x-coordinate of the vertex of the parabola

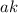`ak` is the y-coordinate of the vertex of the parabola

`a` is a scale factor

For the parabola in the problem, we know that the vertex has coordinates (4,-3), so we have:

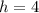`h=4` (2)

`ak=-3`

From this last equation, we get that
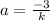`a=(-3)/(k)` (3)

Substituting (2) and (3) into (1) we get the new expression:

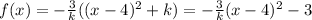`f(x)=-(3)/(k)((x-4)^2+k) = -(3)/(k)(x-4)^2 -3` (4)

We also know that the parabola contains the point (2,-1), so we can substitute

x = 2

f(x) = -1

Into eq.(4) and find the value of k:

`-1=-(3)/(k)(2-4)^2-3\\-1=-(3)/(k)\cdot 4 -3\\2=-(12)/(k)\\k=-(12)/(2)=-6`

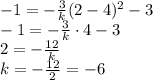
So we also get:

`a=-(3)/(k)=-(3)/(-6)=(1)/(2)`

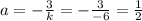
So the equation of the parabola is:

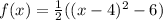`f(x)=(1)/(2)((x-4)^2 -6)` (5)

Now we want to rewrite it in the standard form, i.e. in the form

`f(x)=ax^2+bx+c`

To do that, we simply rewrite (5) expliciting the various terms, we find:

`f(x)=(1)/(2)((x^2-8x+16)-6)=(1)/(2)(x^2-8x+10)=(1)/(2)x^2-4x+5`