Question

You are given three pieces of wire that have different shapes (dimensions). You connect each piece of wire separately to a battery. The first piece has a length L and cross-sectional area A. The second is twice as long as the first, but has the same thickness. The third is the same length as the first, but has twice the cross-sectional area. Rank the wires in order of which carries the most current (has the lowest resistance) when connected to batteries with the same voltage difference.

Answer 1

I3 > I1 > I2

Step-by-step explanation:

Length of first piece = L

Area of first piece = A

Length of second piece = 2L

Area of second piece = A

Length of third piece = L

Area of third piece = 2A

The current is maximum when the resistance is minimum.

Let ρ is the resistivity of the material of wire.

The formula for the resistance is given by

`R = \rho (L)/(A)`

Resistance of first wire

`R_(1) = \rho (L)/(A) = R`

Resistance of second wire

`R_(2) = \rho (2L)/(A)=2R`

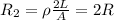
Resistance of third wire

`R_(3) = \rho (L)/(2A)=(R)/(2)`

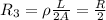
R3 < R1 < R2

I3 > I1 > I2

Thus, the current is maximum in third wire is maximum and minimum in second wire.